Question

Line segments SP has an equation of y=2x+3

What are the other equations of the line segments forming the 3 other sides of the rectangle?

Show work

Answer 1

Answer with Step-by-step explanation:

We are given that

Equation of line segment SP =
`y=2x+3`

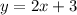
We have to find the equations of the line segments forming the 3 other sides of a rectangle.

Substitute the x=0 in given equation

Then, we get

`y=3`

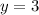
Substitute y=0 then, we get

`0=2x+3`

`2x=-3`

`x=-(3)/(2)=-1.5`

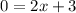
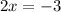
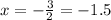
Hence, the equation of line segment SP passing from the point (0,3) and (-1.5,0).

By comparing withe y=mx+c

We get m=2=Slope of line segment SP

The line segment SR is perpendicular to the line segment SP and passing form the point (-1.5,0).

Slope of line segment SR=
`(-1)/(Slope\;of\;SP)=-(1)/(2)`

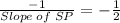
Because when two lines are perpendicular then the relation between the slopes of two lines is given by

`m_2=-(1)/(m_1)`

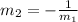
The equation of line segment of SR is given by

`y=m(x-x_1)+y_1`

The equation of line segment SR with slope -1/2 and passing from the point (-1.5,0) is given by

`y=-(1)/(2)(x+1.5)`

`y=-(1)/(2)x-0.75`

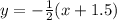
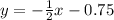
Line segment RQ is parallel to SP

So,Slope of line RQ=2

Because when two lines are parallel then their slope are equal.

Line segment PQ is perpendicular to SP

Therefore, slope of PQ=
`-(1)/(2)`

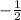
The equation of line segment PQ with slope -1/2 and passing through the point (0,3) is given by

`y=-(1)/(2)(x-0)+3`

`y=-(1)/(2)x+3`

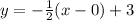
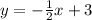
Substitute x=0 in
`y=-(1)/(2)x-0.75`

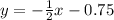
Then, we get y=-0.75

The equation of line segment RQ with slope 2 parallel to SP and passing through the point (0,-0.75)is given by

`y=2x-0.75`