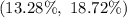Answer:
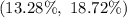
Explanation:
Given : A random sample of 700 home owners in a particular city found 112 home owners who had a swimming pool in their backyard.
i.e. n= 700 and x= 112
Sample proportion :
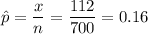
z-value for 95% confidence interval :
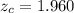
Now, the 95% confidence interval for the true percent of home owners in this city who have a swimming pool in their backyard will be :-
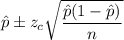
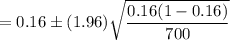
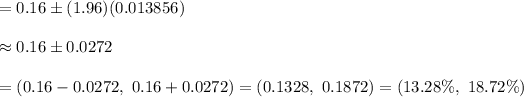
Hence, 95% confidence interval for the true percent of home owners in this city who have a swimming pool in their backyard :