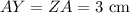Question

Point A is the point of concurrency of the angle bisectors of ΔDEF. Point A is the point of concurrency of triangle D E F. Lines are drawn from each point of the triangle to point A. Lines are drawn from point A to the sides of the triangle to form right angles and line segments A X, A Y, and A Z. The length of F A is 6 centimeters, the length of A D is 5 centimeters, the length of A X is 3 centimeters, and the length of Y D is 4 centimeters.

What is the length of ZA?
A) ZA = 3cm
B) ZA = 4cm
C) ZA = 5cm
D) ZA = 6cm

Answer 1

Answer is A

Explanation:

I just did the test

Answer 2

A) ZA = 3 cm

Explanation:

The triangle is shown below.

From the triangle, A is the concurrency point of angle bisectors of all vertices.

Consider ΔAYD,

Using Pythagorean theorem,

`AD^2=AY^2+ YD^2\\5^2=AY^2+4^2\\25=AY^2+16\\AY^2=25-16\\AY=√(9)=3`

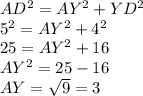
Consider triangles ADY and ADZ.

`\angle AYD\cong \angle AZD=90\\\angle ADY\cong \angle ADZ \textrm{ (angle bisector) }\\AD\cong AD\textrm{ (Common side)}`

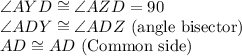
The two triangle are congruent by AAS postulate.

Therefore, by CPCTE,
`AY=ZA=3\textrm{ cm}`