Question

The paraboloid z = 6 − x − x² − 7y² intersects the plane x = 1 in a parabola. Find parametric equations in terms of t for the tangent line to this parabola at the point (1, 2, −24). (Enter your answer as a comma-separated list of equations. Let x, y, and z be in terms of t.)

Answer 1

First you need to know is the equation of the parabola in order to get the equation of the tangent line. So we replace x = 1 in the paraboloid equation and we get:

`z = 6 -1 -1 -7y^(2) \\z = 4 - 7y^(2)`

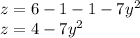
So now that we have the parabola's equation, we calculate the slope of the tangent line deriving and replacing with the point (2,-24) (this point doesn't have the x term because we already used it and we are in terms of y and z).

`z' = -14y\\slope = m = -14*2 = -28`

Now we have the next equation:

`z = -28y + b`

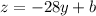
In order to calculate the term 'b', we replace (y,z) with the point (2,-24):

`-24 = -28*2 + b\\b = 32`

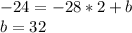
Then, we finally get the tangent line equation as follow:

`z = -28y+32`

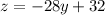
Finally, in order to convert the variables in terms of t, we just replace 't' in any variable. In this case I will replace in y because is convenient.

y = t,

z = -28t+32,

x = 1 (because is always a constant so It doesn't depend of any variable)