Answer:
a). Mileage for carA=
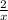 , and mileage for carB=
, and mileage for carB=
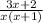
b).total mileage for both is similar to average of them=
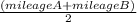
=
![(5x+4)/(2x(x+1))[tex]mil/gal](https://img.qammunity.org/2020/formulas/mathematics/college/1gtkqepigz1nfja454zj44ykx4esdb1yck.png)
Explanation:
It is given that the distance traveled by car
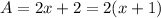
And distance traveled by car
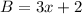
We know the mileage is mile/gallon,
a).So mileage of car
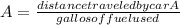
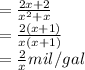
Similarly , the mileage for car
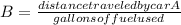
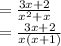
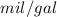
b).total mileage for both is similar to average of them=
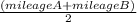
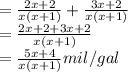
Now divide by 2 for total(average) mileage.
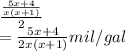 .
.
Thus those are the answers.