Answer:
a) The expected value is 2.680642
b) The minimun number of newspapers the manager should order is 6.
Explanation:
a) Lets call X the demanded amount of newspapers demanded, and Y the amount of newspapers sold. Note that 4 newspapers are sold when at least four newspaper are demanded, but it can be more than that.
X is a random variable of Poisson distribution with mean
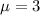, and Y is a random variable with range {0, 1, 2, 3, 4}, with the following values
- PY(k) = PX(k) = ε^(-3)*(3^k)/k! for k in {0,1,2,3}
- PY(4) = 1 -PX(0) - PX(1) - PX(2) - PX (3)
we obtain:
PY(0) = ε^(-3) = 0.04978..
PY(1) = ε^(-3)*3^1/1! = 3*ε^(-3) = 0.14936
PY(2) = ε^(-3)*3^2/2! = 4.5*ε^(-3) = 0.22404
PY(3) = ε^(-3)*3^3/3! = 4.5*ε^(-3) = 0.22404
PY(4) = 1- (ε^(-3)*(1+3+4.5+4.5)) = 0.352768
E(Y) = 0*PY(0)+1*PY(1)+2*PY(2)+3*PY(3)+4*PY(4) = 0.14936 + 2*0.22404 + 3*0.22404+4*0.352768 = 2.680642
The store is expected to sell 2.680642 newspapers
b) The minimun number can be obtained by applying the cummulative distribution function of X until it reaches a value higher than 0.95. If we order that many newspapers, the probability to have a number of requests not higher than that value is more 0.95, therefore the probability to have more than that amount will be less than 0.05
we know that FX(3) = PX(0)+PX(1)+PX(2)+PX(3) = 0.04978+0.14936+0.22404+0.22404 = 0.647231
FX(4) = FX(3) + PX(4) = 0.647231+ε^(-3)*3^4/4! = 0.815262
FX(5) = 0.815262+ε^(-3)*3^5/5! = 0.91608
FX(6) = 0.91608+ε^(-3)*3^6/6! = 0.966489
So, if we ask for 6 newspapers, the probability of receiving at least 6 calls is 0.966489, and the probability to receive more calls than available newspapers will be less than 0.05.
I hope this helped you!