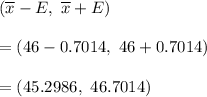Answer with explanation:
Let
 be the population mean .
be the population mean .
Given : Sample size : n=22
Population standard deviation:
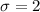
Sample mean :
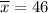
z-value for 91% confidence level :
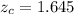
The formula to find the error bound (EBM) :
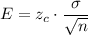
Then , the error bound (EBM) of the confidence interval with a 90% confidence level will be :-
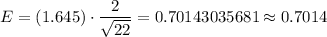
Thus , the error bound (EBM) of the confidence interval with a 90% confidence level: E=0.7014
Furthermore , the 90% confidence interval will be :-