Question

The Daredevil cliffs rise vertically from the beach. The beach slopes gently at an angle of 3 feet from the horizontal. Laying at the water's edge, 50 feet from the base of the cliff, you determine your position, and a straight line to the top of the cliff creates an angle of 70 degrees with the line to the base of the cliff. How high is the daredevil cliff?

Answer 1

160.70 ft. ( approx )

Explanation:

Let AB represents the cliff, C represents Scott's position,

Then according to the question,

m∠ABC = 93°, ( because beach slopes gently at an angle of 3 feet from the horizontal )

m∠ACB = 70°,

BC = 50 ft,

∵ The sum of all interior angles of a triangle is 180°,

i.e. m∠ABC + m∠ACB + m∠BAC = 180°,

⇒ 93° + 70° + m∠BAC = 180°,

⇒ m∠BAC = 180° - 163° = 17°,

By the law of sine,

`(\sin A)/(BC)=(\sin C)/(AB)`

`(\sin 17^(\circ))/(50)=(\sin 70^(\circ))/(AB)`

`\implies AB = (50 sin 70^(\circ))/(sin 17^(\circ))\approx 160.70`

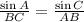
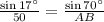
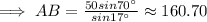
Hence, daredevil cliff is approximately 160.70 ft.