Question

Suppose that in a certain metropolitan area, seven out of 10 households have cable TV. Let x denote the number among six randomly selected households that have cable TV, so x is a binomial random variable with n = 6 and p = 0.7. (Round your answers to four decimal places.)

(a) Calculate p(3) = P(x = 3).
p(3) =

(b) Calculate p(6), the probability that all six selected households have cable TV.
p(6) =

(c) Determine P(x ? 5).
P(x ? 5) =

Answer 1

Answer with Step-by-step explanation:

We are given that

x=The number among six randomly selected household that have cable TV.

n=6, p=0.7

a.We have to calculate p(3)=p(X=3)

Binomial distribution formula :
`P(X=x)=nC_xp^xq^(n-x)`

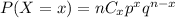
q=1-p=1-0.7=0.3

`P(X=3)=6C_3(0.7)^3(0.3)^3=(6!)/(3!3!)(0.7)^3(0.3)^3`

`P(X=3)=(6* 5* 4* 3!)/(3!3* 2* 1)(0.7)^3(0.3)^3=0.1852` (
`nC_r=(n!)/(r!(n-r)!)`)

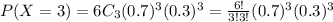
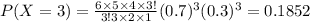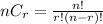P(X=3)=0.1852

b.We have to calculate p(6)

`P(X=6)=6C_6(0.7)^6=0.1176`

`P(X=6)=0.1176`

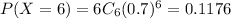
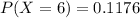
Hence, the probability that all six household have cable TV=0.1176

c P(X=5)=
`6C_5(0.7)^5(0.3)`

`P(X=5)=(6!)/(5!)(0.7)^5(0.3)=(6* 5!)/(5!)(0.7)^5(0.3)=0.3025`

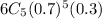
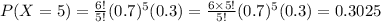
Hence, P(X=5)=0.3025