Answer: 1692
Explanation:
Formula to find the sample size :
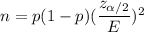
Given : Confidence level :
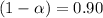
⇒ significance level =
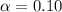
z-value for 90% confidence interval (using z-table)=
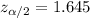
Prior estimate of the population proportion (p) of customers who keep up with regular vehicle maintenance is unknown.
Let we take p= 0.5
Margin of error : E= 2%=0.02
Now, the required sample size will be :
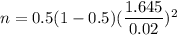
Simplify , we get
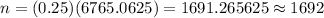
Hence, the required sample size = 1692