Question

Two gliders with different masses (m1 and m2) are placed on a frictionless air track and given initial velocities v1i and v2i. They elastically collide, bouncing off each other. (a) Determine the equations for the final velocity of each glider. (b) For m1 = 0.51 kg, m2 = 0.98 kg, v1i=1.5 im/s, and v2i=-2.2 im/s, find v1f and v2f.

Answer 1

(a)

vf₁ = (m₁*v₀₁+2m₂v₀₂- m₂v₀₁) / ( m₁+ m₂)

vf₂ = (v₀₁ - v₀₂ ) + ((m₁*v₀₁+2m₂v₀₂- m₂v₀₁) / ( m₁+ m₂))

(b)

vf₁ = - 3.367 m/s

vf₂ = 0.333 m/s

Step-by-step explanation:

Theory of collisions

Linear momentum is a vector magnitude (same direction of the velocity) and its magnitude is calculated like this:

p=m*v

where

p:Linear momentum

m: mass

v:velocity

There are 3 cases of collisions : elastic, inelastic and plastic.

For the three cases the total linear momentum quantity is conserved:

P₀ = Pf Formula (1)

P₀ :Initial linear momentum quantity

Pf : initial linear momentum quantity

Nomenclature

m₁ : mass of the first glider

m₂ : mass of the second glider

v₀₁:initial velocity of m₁

v₀₂ :initial velocity of m₂

vf₁: final velocity of m₁

vf₂: final velocity of m₂

Data

m₁,m₂,v₀₁i,v₀₂i

Problem development

(a) We appy the formula (1):

Because the initial and final velocities are in the same direction (i), (i) is canceled in the equation:

P₀ = Pf

m₁*v₀₁ + m₂*v₀₂ = m₁*vf₁ + m₂*vf₂ Equation( 1)

Because the shock is elastic, the coefficient of elastic restitution (e) is equal to 1.

`e=(v_(f2) -v_(f1))/(v_(o1) -v_(o2))`

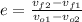
(equation 1)

vf₂ = (v₀₁ - v₀₂ ) + vf₁ Equation( 2)

We replace Equation( 2) in Equation( 1)

m₁*v₀₁ + m₂*v₀₂ = m₁*vf₁ + m₂* ((v₀₁ - v₀₂ ) + vf₁ )

m₁*v₀₁ + m₂*v₀₂ = m₁*vf₁ + m₂*v₀₁ - m₂ v₀₂ + m₂vf₁

m₁*v₀₁ + m₂*v₀₂ + m₂ v₀₂ - m₂*v₀₁= m₁*vf₁ + m₂vf₁

m₁*v₀₁+2m₂v₀₂- m₂v₀₁ = vf₁( m₁+ m₂)

vf₁ = (m₁*v₀₁+2m₂v₀₂- m₂v₀₁) / ( m₁+ m₂) Equation (3)

vf₂ = (v₀₁ - v₀₂ ) + vf₁

vf₂ = (v₀₁ - v₀₂ ) + ((m₁*v₀₁+2m₂v₀₂- m₂v₀₁) / ( m₁+ m₂)) Equation (4)

(b) Data

m₁, = 0.51 kg

m₂ = 0.98 kg

v₀₁,= 1.5 im/s

v₀₂ = -2.2 im/s

We replace data in the Equation (3) to calculate vf₁

vf₁ = (m₁*v₀₁+2m₂v₀₂- m₂v₀₁) / ( m₁+ m₂)

vf₁ = ( 0.51)* ( 1.5)+2 ( 0.98) ( -2.2) -(0.98) ( 1.5) / ( 0.51+ 0.98)

vf₁ = -3.367 m/s

We replace data in the Equation (2) to calculate vf₂

vf₂ = (v₀₁ - v₀₂ ) + vf₁

vf₂ = (1.5 -(-2.2 ) +(-3.367)

vf₂ = (1.5+2.2 ) -3.367

vf₂ = 0.333 m/s