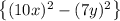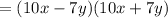Question

Which expression is a difference of squares?

100x^2-55y^2
100x^2+55y^2
100x^2+49y^2
100x^2-49y^2

Answer 1

Answer: 100
`x^(2)` - 49
`y^(2)`

Explanation:

Answer 2

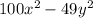`100 x^(2)-49 y^(2)` can be written in the difference of squares.

Option: D

Explanation:

We know that
`a^(2)-b^(2)=(a-b)(a+b)`

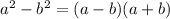
Take the equation
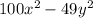`100 x^(2)-49 y^(2)` and can be written as follows.

`\left(100 x^(2)-49 y^(2)\right)=\left\{(10 x)^(2)-(7 y)^(2)\right\}`

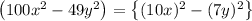
100 is the square of 10

49 is the square of 7

`x^(2)` is the square of x

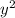`y^(2)` is the square of y

Thus we can write the
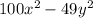`100 x^(2)-49 y^(2)` as the difference of squares.

`\left(100 x^(2)-49 y^(2)\right)=\left\{(10 x)^(2)-(7 y)^(2)\right\}`

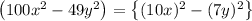
By using the formula
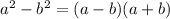`a^(2)-b^(2)=(a-b)(a+b)` we can write
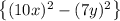`\left\{(10 x)^(2)-(7 y)^(2)\right\}` as

`\left\{(10 x)^(2)-(7 y)^(2)\right\}`
`=(10 x-7 y)(10 x+7 y)`