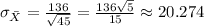Question

The operating costs for each machine for one day have an unknown distribution with mean 1610 and standard deviation 136 dollars. A sample, with size n=45, was randomly drawn from the population. Using the Central Limit Theorem for Means.

What is the standard deviation for the sample mean distribution?

Answer 1

The standard deviation for the sample mean distribution is
`\sigma_{\bar{X}}=(136)/(√(45))=(136√(5))/(15) \approx 20.274`

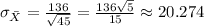
Explanation:

The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population then the distribution of the sample means will be approximately normally distributed.

For the random samples we take from the population, we can compute the standard deviation of the sample means:

`\sigma_{\bar{X}}=(\sigma)/(√(n))`

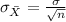
From the information given

The standard deviation σ = 136 dollars

The sample n = 45

Thus,

`\sigma_{\bar{X}}=(136)/(√(45))=(136√(5))/(15) \approx 20.274`

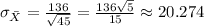
The standard deviation for the sample mean distribution is
`\sigma_{\bar{X}}=(136)/(√(45))=(136√(5))/(15) \approx 20.274`