Answer with explanation:
According to the Binomial probability distribution ,
Let x be the binomial variable .
Then the probability of getting success in x trials , is given by :
 , where n is the total number of trials or the sample size and p is the probability of getting success in each trial.
, where n is the total number of trials or the sample size and p is the probability of getting success in each trial.
As per given , we have
n = 15
Let x be the number of defective components.
Probability of getting defective components = P = 0.03
The whole batch can be accepted if there are at most two defective components. .
The probability that the whole lot is accepted :
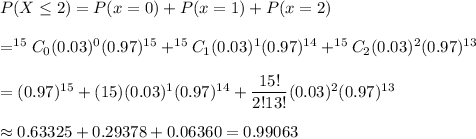
∴The probability that the whole lot is accepted = 0.99063
For sample size n= 2500
Expected value :
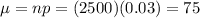
The expected value = 75
Standard deviation :
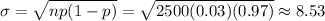
The standard deviation = 8.53