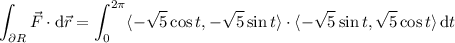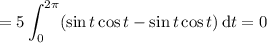Looks like we're given
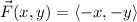
which in three dimensions could be expressed as
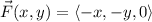
and this has curl
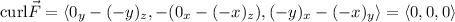
which confirms the two-dimensional curl is 0.
It also looks like the region
 is the disk
is the disk
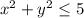 . Green's theorem says the integral of
. Green's theorem says the integral of
 along the boundary of
along the boundary of
 is equal to the integral of the two-dimensional curl of
is equal to the integral of the two-dimensional curl of
 over the interior of
over the interior of
 :
:
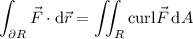
which we know to be 0, since the curl itself is 0. To verify this, we can parameterize the boundary of
 by
by
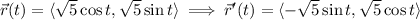
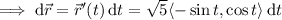
with
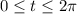 . Then
. Then