Question

Write the point-slope form of the equation of the line through point (6, -2) that is perpendicular to the line y=2x-3​

Answer 1

The point - slope form of the equation of line 1 is y = (-1/2)x + 1

Explanation:

here, the given point on the equation 1 is A(6, -2).

Now, equation of line 2 is y = 2x - 3

Comparing it with the INTERCEPT SLOPE FORM : y = mx + C

Slope of Line 2 = 2 (= m2)

Now,as line 1 is perpendicular to line 1

⇒ Slope of line 1 x Slope of line 2 = -1

or, slope of line 1 = (-1/2)

Now, by POINT SLOPE form of a equation:

An equation with point (x0 , y0) and slope m is given as

(y - y0)= m (x - x0)

Here, the equation of line 1 with point (6, -2) and slope (-1/2) is given as:

`y - (-2)  = (-1)/(2)  (x -6)\\\implies 2( y + 2)   = 6 -x\\or, 2y + 4  = 6 -x\\\implies 2y = -x + 2\\or, y = (-(1)/(2)) x + 1`

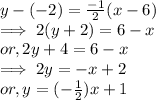
Hence, the point - slope form of the equation of line 1 is y = (-1/2)x + 1