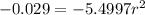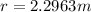Question

A drag racing car with a weight of 1600 lbf attains a speed of 270 mph in a quarter-mile race. Immediately after passing the timing lights, the driver opens a drag chute. At this point, the air and rolling resistance of the car are negligible compared to the drag of the chute. What chute diameter (in feet) is required to make sure that the car decelerates to 60 mph within 7 seconds?

Answer 1

15.065ft

Step-by-step explanation:

To solve this problem it is necessary to consider the aerodynamic concepts related to the Drag Force.

By definition the drag force is expressed as:

`F_D = -(1)/(2)\rho V^2 C_d A`

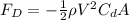
Where

`\rho` is the density of the flow

V = Velocity

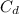`C_d`= Drag coefficient

A = Area

For a Car is defined the drag coefficient as 0.3, while the density of air in normal conditions is 1.21kg/m^3

For second Newton's Law the Force is also defined as,

`F=ma=m(dV)/(dt)`

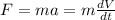
Equating both equations we have:

`m(dV)/(dt)=-(1)/(2)\rho V^2 C_d A`

`m(dV)=-(1)/(2)\rho C_d A (dt)`

`(1)/(V^2 )(dV)=-(1)/(2m)\rho C_d A (dt)`

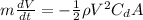
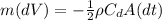
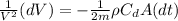
Integrating

`\int (1)/(V^2 )(dV)= - \int(1)/(2m)\rho C_d A (dt)`

`-(1)/(V)\big|^(V_f)_(V_i)=(1)/(2m)(\rho)C_d (\pi r^2) \Delta t`

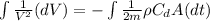
Here,

`V_f = 60mph = 26.82m/s`

`V_i = 120.7m/s`

`m= 1600lbf = 725.747Kg`

`\rho = 1.21 kg/m^3`

`C_d = 0.3`

`\Delta t=7s`

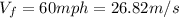
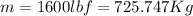
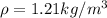
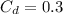
Replacing:

`(-1)/(26.82)+(1)/(120.7) = (1)/(2(725.747))(1.21)(0.3)(\pi r^2) (7)`

`-0.029 = -5.4997r^2`

`r = 2.2963m`

`d= r*2 = 4.592m \approx 15.065ft`