Answer:
Part a)
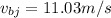
Part b)
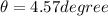 East of South
East of South
Step-by-step explanation:
Part a)
Velocity of Juan is given as
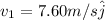
velocity of the ball is given as
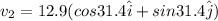
now we have
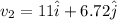
Part a)
We need to find velocity of ball with respect to Juan
so it is given as
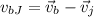
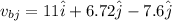
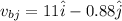
magnitude of the speed is given as
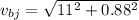
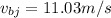
Part b)
direction of velocity of the ball
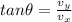
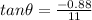
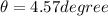 East of South
East of South