Question

Two buses leave a station at the same time and travel in opposite directions. One bus travels 9 mi h slower than the other. If the two buses are 585 miles apart after 5 hours, what is the rate of each bus?

Answer 1

The speed of bus 1 is 63 mile per hour And bus 2 is 54 mile per hour

Explanation:

According to question

Let the speed of bus 1 =
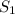`S_1` = S mph

and The sped of bus 2 =
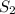`S_2` = S - 9 mph

Let The distance travel by bus 1 =
`D_1` = D mile

And The distance travel by bus 2 =
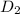`D_2` = ( 585 - D ) mile

he time taken by both buses to cover distance = T hour

Now, Distance = Speed × Time

So ,
`D_1` =
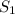`S_1` × T

Or, D = S × T ......... 1

Again
`D_2` =
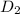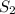`S_2` × T

Or, ( 585 - D ) = ( S - 9 ) × T ..........2

From eq 1 an eq 2

585 - S ×T = S ×T - 9 T

Or, 585 + 9 T = 2 × S ×T

Or, 585 + 9 × 5 = 2 × S × 5

Or, 585 + 45 = 10 × S

So , 630 = 10 × S

∴ S =
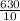`(630)/(10)` = 63 mph

And S -9 = 63 - 9 = 54 mph

Hence The speed of bus 1 is 63 mile per hour And bus 2 is 54 mile per hour Answer

Answer 2

The speed of the buses are 58.2 mph and 49.2 mph.

Explanation:

Let the speed of bus 1 is x mph.

So, the other bus 2 has speed (x - 9) mph.

Then time-traveled to cover 585 miles by bus 1 will be
`(585)/(x)` hours.

Again time-traveled to cover 585 miles by bus 2 will be
`(585)/(x - 9)` hours.

Therefore, from the condition given

`(585)/(x - 9) - (585)/(x) = 9`

⇒
`65((1)/(x-9) -(1)/(x)) = 1`

⇒
`x^(2) - 9x - 585 = 0`

Applying the Sridhar Acharya formula

`x = \frac{9+\sqrt{9^(2)- 4 * (-585) } }{2}` {Neglecting the negative root}

⇒ x = 58.2 mph

So, x - 9 = 49.2 mph

Therefore, the speed of the buses are 58.2 mph and 49.2 mph. (Answer)