Question

3. How many lists of length 3 can be made from the symbols A, B, C, D, E, F if... (a) ... repetition is allowed. (b) ... repetition is not allowed. (c) ... repetition is not allowed and the list must contain the letter A. (d) ... repetition is allowed and the list must contain the letter A.

Answer 1

a) 216 possible lists.

b) 20 possible lists.

c) 10 possible lists.

d) 91 possible lists.

Explanation:

(a) If repetition is allowed, then we have to form triplets (x,y,z) where each position has 6 possibilities (A, B, C, D, E, F).

By the Fundamental Rule of counting there are

6*6*6 = 216 possible lists.

(b) If repetition is not allowed, then there are combinations of 6 taken 3 at a time

`\bf \binom{6}{3}=(6!)/(3!(6-3)!)=(6!)/(3!3!)=20`

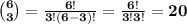
possible lists.

(c) If repetition is not allowed and the list must contain the letter A.

In this case we have to subtract from 20 all the triplets that have no A. There are combinations of 5 (B, C, D, E, F ) taken 3 at a time triplets with no A.

`\bf \binom{5}{3}=(5!)/(3!(5-3)!)=(5!)/(3!2!)=10`

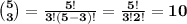
hence there are 20-10=10 possible lists.

(d) If repetition is allowed and the list must contain the letter A.

In this case we have to subtract from the 216 obtained in (a) the triplets that have no A.

By the Fundamental Rule of counting there are

5*5*5 = 125 triplets without the A.

Hence there are 216-125=91 possible lists.