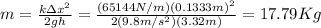Question

A scene in a movie has a stuntman falling through a floor onto a bed in the room below. The plan is to have the actor fall on his back, but a researcher has been hired to investigate the safety of this stunt. When the researcher examines the mattress, she sees that it effectively has a spring constant of 77144 N/m for the area likely to be impacted by the stuntman, but it cannot depress more than 13.33 cm without injuring him. To approach this problem, consider a simplified version of the situation. A mass falls through a height of 3.32 m before landing on a spring of force constant 65144 N/m. Calculate the maximum mass that can fall on the mattress without exceeding the maximum compression distance.

Answer 1

`m=17.79Kg`

Step-by-step explanation:

In this process energy must be conserved. On the initial stage, there will be only gravitational potential energy, while on the final stage there will be only elastic potential energy, so they will be equal. We write this as:

`U_g=U_e`

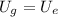
Which is the same as:

`mgh=(k \Delta x^2)/(2)`

So we can obtain our mass from there, and for our values:

`m=(k \Delta x^2)/(2gh)=((65144 N/m)(0.1333m)^2)/(2(9.8m/s^2)(3.32m))=17.79Kg`