Question

Graph the system of equations on your graph paper to answer the question

Sy=-x+3
(y=x+5
SEBE
What is the solution for this system of equations?
Enter your answer in the boxes.

Answer 1

Since we have to solve this system graphically, we'll have to draw both lines.

To draw a line, simply build a little tables with two x,y values: for the first line we have

`\begin{array}cx&-x+3\\0&3\\1&2\end{array}`

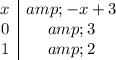
So, you can draw the points (0,3) and (1,2), connect them, and you'll have the graph of the line
`y=-x+3`

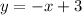
For the second line we have

`\begin{array}cx&x+5\\0&5\\1&6\end{array}`

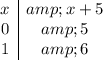
So, you can draw the points (0,5) and (1,6), connect them, and you'll have the graph of the line
`y=x+5`

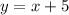
Finally, we have to check where the two lines cross. If your drawing is accurate enough, you'll see that the point you're looking for is (-1, 4)