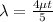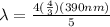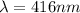Question

What visible wavelengths of light are strongly reflected from a 390-nm-thick soap bubble?

Answer 1

So visible wavelength which is possible here is

416 nm and 693.3 nm

Step-by-step explanation:

As we know that for normal incidence of light the path difference of the reflected ray is given as

`2\mu t + (\lambda)/(2) = \Delta x`

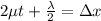
so here we can say that for maximum intensity condition we will have

`\Delta x = N\lambda`

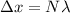
so we have

`2\mu t + (\lambda)/(2) = N\lambda`

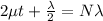
now for visible wavelength we have

for N = 1

`2\mu t = (\lambda)/(2)`

`\lambda = 4\mu t`

`\lambda = 4((4)/(3))(390 nm)`

`\lambda = 2080 nm`

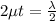
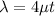
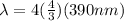
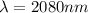
for N = 2

`\lambda = (4\mu t)/(3)`

`\lambda = (4((4)/(3))(390 nm))/(3)`

`\lambda = 693.3 nm`

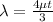
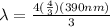
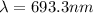
for N = 3

`\lambda = (4\mu t)/(5)`

`\lambda = (4((4)/(3))(390 nm))/(5)`

`\lambda = 416 nm`