Question

A store sells both cold and hot beverages. Cold beverages, c, cost $1.50, while hot beverages, h, cost $2.00. On Saturday, drink receipts totaled $360, and 4 times as many cold beverages were sold as hot beverages.

Part 1: Write a system of equations to represent the beverage sales on Saturday.

Part 2: Use any solving method you like to solve the system of equations you wrote in Part 1. Show all of your work.

Answer 1

Equation:

`4(1.50b) + 2b = 360`

Explanation:

`6b+2b=360\\8b=360\\b=45`

They sold 45 Hot Beverages and 180 Cold Beverages

Answer 2

180 cold beverages and 45 hot beverages were sold

Explanation:

Let x be the no. of cold beverages were sold

Let y be the no. of hot beverages were sold

We are given that On Saturday, 4 times as many cold beverages were sold as hot beverages.

So, x=4y

Cost of 1 cold beverage = $1.50

Cost of x cold beverage = 1.50x

Cost of 1 hot beverage = $2.00.

Cost of y hot beverage = 2y

On Saturday, drink receipts totaled $360

So,
`1.50x+2y=360`

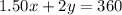
A system of equations to represent the beverage sales on Saturday:

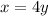`x=4y` ---1

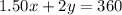`1.50x+2y=360` ---2

Substitute the value of x from 1 in 2

`1.50(4y)+2y=360`

`6y+2y=360`

`8y=360`

`y=45`

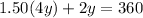
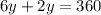
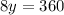
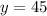
Substitute the value of y in 1

`x=4(45)`

`x=180`

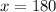
Hence 180 cold beverages and 45 hot beverages were sold