Answer:
5.03 m
Step-by-step explanation:
Let the distance of burglar from the top of window be
 m.
m.
Given:
Displacement of the bag while passing the window,
 m
m
Time to cross the window,
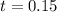 s
s
Acceleration due to gravity,
 m/s²(∵ it acts down)
m/s²(∵ it acts down)
Negative sign indicates downward motion and hence negative.
We find the velocity of the bag at the top of the window using Newton's equation of motion for displacement.
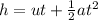
Where,
 is the velocity at the top of window.
is the velocity at the top of window.
Now, plug in all the known values and solve for
 .
.
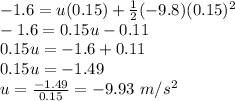
Now, from the point of drop to the top of the window, displacement is
 . Initial velocity is zero as it is dropped. Acceleration is due to gravity. Final velocity is velocity at the top of window which is equal to -9.93 m/s².
. Initial velocity is zero as it is dropped. Acceleration is due to gravity. Final velocity is velocity at the top of window which is equal to -9.93 m/s².
Therefore, using Newton's equation of motion
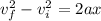 , we find
, we find
 .
.
Here,
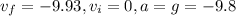
Therefore,
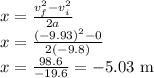
The negative sign indicates that the bag is falling down.
So, the bag is dropped at a height of 5.03 m from above the top of the window.