Question

You are exiting a highway and need to slow down on the off-ramp in order to make the curve. It is rainy and the coefficient of static friction between your tires and the road is only 0.25. If the radius of the off-ramp curve is 40 m, then to what speed do you need to slow down the car in order to make the curve without sliding?

Please explain how to do it.

Answer 1

Speed = 9.9 m/s

Step-by-step explanation:

Given:

Coefficient of static friction is,
`\mu=0.25`

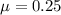
Radius of the curve,
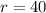`r=40` m

Let the speed that has to be reached be
`v` m/s.

In order to avoid sliding while making a turn, the frictional force provides the necessary centripetal force.

We know that, frictional force acting on a body is given as:

`f=\mu N=\mu mg` (
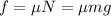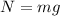`N=mg` as there is no vertical motion)

Also, from the definition of centripetal force,

`f=(mv^2)/(r)`

On equating the above two equations, we get

`(mv^2)/(r)=\mu mg\\v^2=\mu gr\\v=√(\mu gr)`

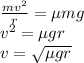
Now, plug in 0.25 for
`\mu`, 9.8 for
`g` and 40 for
`r`.

`v=√(0.25* 9.8* 40)\\v=√(98)=9.9\textrm{ m/s}`

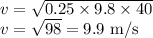
Therefore, speed of the car has to be slowed down to minimum of 9.9 m/s in order to avoid sliding while making a turn.