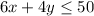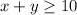Answer:
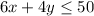
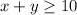
Explanation:
 represents the number of stuffed animals.
represents the number of stuffed animals.
 represents the number of toy trucks.
represents the number of toy trucks.
Now, according to the problem, she found stuffed animals for $6.00 each and toy trucks for $4.00 each. Also, Laura has a restricted budget of $50. All these can be expressde as
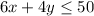
Also, the problem states that Laura wants to provide one partu favor per person to at least 10 people, that means
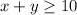 , because "at least" represents a minimum value, which is expressed with
, because "at least" represents a minimum value, which is expressed with
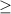 .
.
Therefore, the inequality system that models this situation is