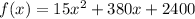Question

Joe wants to enlarge the rectangular pumpkin patch located on his farm. The pumpkin patch is currently 40 meters wide and 60 meters long. The new pumpkin patch will be 3x meters wider and 5x meters longer than that of the original pumpkin patch. Which of the following functions will give the area of the new pumpkin patch in square meters?

Answer 1

What he said is correct above.

Explanation:

Answer 2

`15x^2+380x+2400`

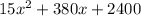
The diagram is shown below for reference.

Explanation:

We are given the length and width of old pumpkin patch as
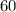`60` meters and
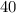`40` meters respectively.

It further says length is increased by
`5x` meters and width increased by
`5x` meters.

So the length of the new pumpkin patch would be
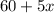`60+5x` meters.

And the width would be
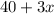`40+3x` meters.

We know area of a rectangular shape
`=length * width`

So, plugging the above values, we get the area of the new pumpkin patch as:

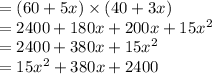`=(60+5x)* (40+3x)\\=2400+180x+200x+15x^2\\=2400+380x+15x^2\\=15x^2+380x+2400` on rearranging.

Thus the function of the area of the new pumpkin patch would be:

`f(x) = 15x^2+380x+2400`