Let x be the total number of people who could have voted. We know that 4/25 didn't vote, so the actual number of people who voted is the remaining 21/25 of x.
Out of these people, 4/7 voted for the winner:
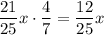
We know that this fraction resulted in 4956 votes, solving for x we have
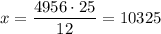
So, 10325 people could have voted. But we know that 4/25 didn't vote, while the remaining 21/25 did. So, the number of voters who took part to the election is
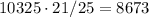
Just for checking, we have indeed
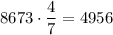
which confirms the result.