Answer:
4000
Explanation:
THe formula given is:
T = UN + F
Where T is the total cost
U is the cost per unit
N is the number of units manufactured
F is the fixed cost
Also, in the problem, it is given,
F = 5000
U = 15
T = 65000
We need to find N, the number of clocks, so lets rearrange the formula so that we have N = SOMETHING:

Now we substitute the given information into this to find N:
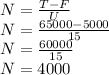
So,
number of clocks made = 4000