Question

In 1940, there were about 10 brown tree snakes per square mile on the island of Guam, and in 1980, there were about 5000 per square mile.

(a) Find an exponential formula for the number, N, of brown tree snakes per square mile on Guam t years after 1940.
N=

(b) On average, what was the annual percent increase in the population during this period? (Round to nearest 0.01%)

Answer 1

a)
`500=(1+r)^(40)`

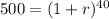
b) 16.81%

Explanation:

a)

The general formula for compound growth is:

`F=P(1+r)^t`

Where

F is the future amount (5000 in our case)

P is the present amount (10 here)

r is the rate of growth (we don't know that yet)

t is the time in years (that would be 1980 - 1940 = 40)

So, the formula becomes:

`F=P(1+r)^t\\5000=10(1+r)^(40)\\500=(1+r)^(40)`

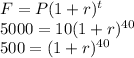
b)

We need to find the growth rate (annual percentage increase). So we have to solve for "r" in the equation found in part (a).

`500=(1+r)^(40)\\\sqrt[40]{500} =\sqrt[40]{(1+r)^(40)} \\1.1681=1+r\\r = 1.1681 - 1 = 0.1681`

To get percentage, we multiply by 100:

0.1681 * 100 = 16.81%