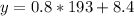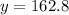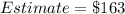Question

A lemonade seller calculates that it costs $ to produce glass of lemonade and $ to produce glass of lemonade. Assume the relationship between the cost and the number of glass of lemonade produced is linear. What is the most reasonable estimate for producing glass of lemonade

Answer 1

Question:

A lemonade seller calculates that it costs $50 to produce 52 glass of lemonade and $110 to produce 127 glass of lemonade. Assume the relationship between the cost and the number of glass of lemonade produced is linear. What is the most reasonable estimate for producing 193 glass of lemonade?

Answer:

`(a).\ y = 0.8x + 8.4`

`(b).\ Estimate = \$163`

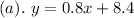
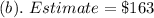
Explanation:

Represent number of lemonade with x and the cost with y.

So:

`(x_1,y_1) = (52,50)`

`(x_2,y_2) = (127,110)`

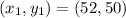
Solving (a): The linear relationship between them.

First, calculate slope (m)

m = ∆y ÷ ∆x

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (110 - 50)/(127 - 52)`

`m = (60)/(75)`

`m = 0.8`

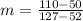
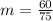
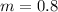
The equation is then calculated as:

`y - y_1 = m(x - x_1)`

This gives:

`y - 50 = 0.8(x - 52)`

`y - 50 = 0.8x - 41.6`

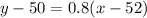
Make y the subject

`y = 0.8x - 41.6 + 50`

`y = 0.8x + 8.4`

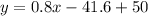
Solving (b): Estimate of 193 lemonade

In (a), we have:

`y = 0.8x + 8.4`

Substitute 193 for x

`y = 0.8 * 193 + 8.4`

`y = 154.4 + 8.4`

`y = 162.8`

`Estimate = \$163`