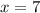Question

Please help it would be much appreciated :)

Answer 1

Value of
`x=7`

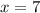
Explanation:

By applying proportionality theorem we know that length of corresponding sides of similar triangles are proportional.

From the figure we can set up the ratio of the sides assuming Tiangle ABC is similar to Triangle DEF:

`(AB)/(DE)=(BC)/(EF)=(AC)/(DF) \\\\(4)/(12)=(x-1)/(18) =(8)/(3x+1)`

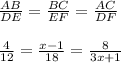
Now, we can solve for x by using two of the ratios.

`(x-1)/(18) =(4)/(12)`

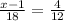
Reducing to simpler fraction.

`(x-1)/(18) =(4/4)/(12/4) =(1)/(3)`

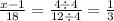
Using cross multiplication.

`3(x-1)=18*1\\`

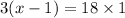
Dividing both sides by 3.

`(3(x-1))/(3) =(18)/(3) \\x-1=6`

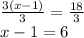
Adding 1 to both sides.

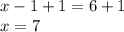
`x-1+1=6+1\\x=7`

∴
`x=7`