Answer: (0,1)
Explanation:
If
 and
and
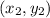 are two point son a coordinate plane and (x,y) dividing it in a ratio of m: n.
are two point son a coordinate plane and (x,y) dividing it in a ratio of m: n.
Then , the coordinates of (x,y) is given by :-
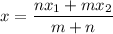
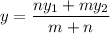
Given : On a coordinate plane, a line is drawn from point A to point B. Point A is at (2, - 3) and point B is at (- 4, 9).
Then , the x- and y- coordinates of point E, which partitions the directed line segment from A to B into a ratio of 1:2 :

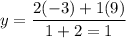
Hence, the x- and y- coordinates of point E = (0,1)