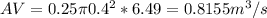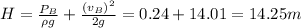Answer:
Height=14.25 m
Discharge=
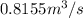
Step-by-step explanation:
Bernoulli’s equation for the two points, let’s say A and B is given by
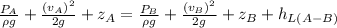
But since the elevations are the same then
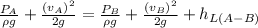
Since
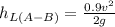 then
then
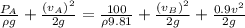
From continuity equation
![A_AV_A=A_BV_B=0.25\pi D^(2)V_A=0.25\pi d^(2)V_B hence [tex]D^(2)V_A= d^(2)V_B](https://img.qammunity.org/2020/formulas/engineering/college/68tuznw0emgd3xodlxseet0n5qntm0lcl5.png) and substituting 0.4 for D and 0.25 for d
and substituting 0.4 for D and 0.25 for d
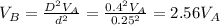
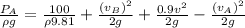 and substituting
and substituting
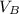 with
with
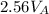 we have
we have
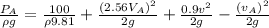
Since
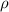 is taken as 1 then
is taken as 1 then
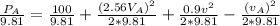
v=6.49 m/s
Since discharge=