The moment of inertia (J) is
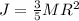
How to determine the moment of inertia?
When an object descends from a height \(h\), it loses potential energy,
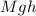 , and gains kinetic energy,
, and gains kinetic energy,
 , where
, where
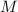 is the mass of the object and
is the mass of the object and
 is its velocity.
is its velocity.
Additionally, it acquires rotational kinetic energy,
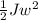 , where
, where
 is the moment of inertia and
is the moment of inertia and
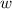 is the angular speed (
is the angular speed (
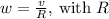 being the radius of rotation).
being the radius of rotation).
By equating the energies:
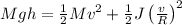 , and further simplifying:
, and further simplifying:
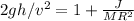
We know
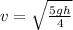 . Thus,
. Thus,
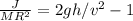 .
.
Solving for
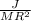 :
:
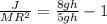 , therefore
, therefore
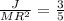 .
.
Consequently,
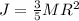 .
.