Answer:
The rate at which amount of photo increase after 6 days is 7.75
Explanation:
Given as :
The original amount of photo = 44
The final amount of photo = 44 + 25 = 69
Time period = 6 days
Let The rate = r
So, final value after n days = original value ×
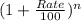
Or, 69 = 44 ×
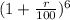
Or,
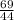 =
=
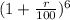
Or, 1.568 =
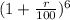
Or,
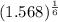 =
=

Or, ( 1.0775 - 1 ) × 100 = r
Or, 0.0775 × 100 = r
∴ r = 7.75
Hence The rate at which amount of photo increase after 6 days is 7.75 Answer