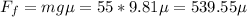Answer:
(a)11.24 m/s
(b)7.44 m/s
(c)409 N
(d)
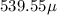
(e) 0
Step-by-step explanation:
The period for 1 circle
 of the merry go around is 9.5s. It means the angular speed is:
of the merry go around is 9.5s. It means the angular speed is:
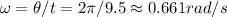
(a)The speed is
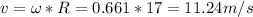
(b) Centripetal acceleration:
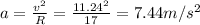
(c) Magnitude of the force that keeps you go around at this acceleration
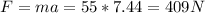
(d) let the coefficient of friction by
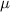 . The frictional force shall be this coefficient multiplied by normal force reverting gravity of the man
. The frictional force shall be this coefficient multiplied by normal force reverting gravity of the man