Question

A produce distributor uses 774 packing crates a month, which it purchases at a cost of $12 each. The manager has assigned an annual carrying cost of 34 percent of the purchase price per crate. Ordering costs are $29. Currently the manager orders once a month. How much could the firm save annually in ordering and carrying costs by using the EOQ?

Answer 1

annual saving = $444.42

Step-by-step explanation:

given data

monthly demand = 774

purchases cost = $12

annual carrying cost = 34 % of the purchase price

Ordering costs = $29

solution

we know here annual demand will be = 774 × 12 = 9288 crates

and

carrying cost = 34 % of $12 = $4.08

so

economic order quantity Q will be

Q =
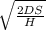`\sqrt{(2DS)/(H)}` .................1

here D is annual demand and S is ordering cost and H is carrying cost

so put the value we get

Q =
`\sqrt{(2*9288*29)/(4.08)}`

Q = 363.37 = 363 creates

and

total annual cost with EOQ will be

total annual cost = annual carrying cost + annual ordering cost ...............2

total annual cost =
`(Q)/(2) H + (D)/(Q) S`

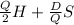
put here value we get

total annual cost =
`(363)/(2) 4.08 + (9288)/(363) 29`

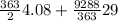
total annual cost = 740.52 + 742.02

total annual cost = $1482.54

so

order quantity = monthly demand = 774 crates

so total annual cost with current policy is

total annual cost is = annual carrying cost + annual ordering cost

total annual cost is =
`(Q)/(2) H + (D)/(Q) S`

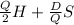
put here value we get

total annual cost =
`(774)/(2) 4.08 + (9288)/(774) 29`

total annual cost = 1578.96 + 348

total annual cost = $1926.96

so

annual saving = total annual cost with current policy - total annual cost with EOQ

annual saving = $1926.96 - $1482.54

annual saving = $444.42