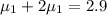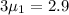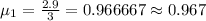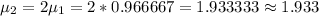Answer:
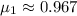
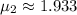
Step-by-step explanation:
The viscosities above and below the plate are given by
 where
where
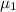 and
and
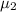 are viscosities of fluid below and above plate respectively
are viscosities of fluid below and above plate respectively
Force on plate due to top layer of the fluid
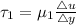 where
where
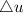 and
and
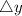 are the velocity of plate and gap between the plate and upper surface respectively.
are the velocity of plate and gap between the plate and upper surface respectively.
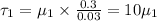
Force on plate due to bottom layer of the fluid is given by
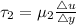 where
where
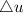 and
and
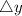 are the velocity of plate and gap between the plate and upper surface respectively
are the velocity of plate and gap between the plate and upper surface respectively

Total force per unit area is the sum of two shear forces
 hence
hence
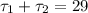
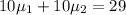
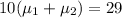
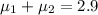 but since
but since
 hence
hence