Question

A 2.4 m long wire weighing 0.127 N/m is suspended directly above an infinitely straight wire. The top wire carries a current of 29 A and the bottom wire carries a current of 37 A . The permeablity of free space is 1.25664 × 10−6 N/A 2 . Find the distance of separation between the wires so that the top wire will be held in place by magnetic repulsion.

Answer 1

`d=1.68* 10^(-3)\ m`

Step-by-step explanation:

It is given that,

Length of the wire, l = 2.4 m

Force per unit length of the wire,
`(F)/(l)=0.127\ N/m`

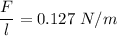
Current in top wire,
`I_1=29\ A`

Current in bottom wire,
`I_2=37\ A`

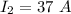
The permeability of free space is,
`\mu_o=1.25664* 10^(-6)\ N/m^2`

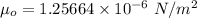
Let d is the distance of separation between the wires so that the top wire will be held in place by magnetic repulsion. The magnetic force per unit length is given by :

`(F)/(L)=(\mu_o I_1I_2)/(2\pi d)`

`d=(\mu_o I_1I_2)/(2\pi F/L)`

`d=(1.25664* 10^(-6)* 29* 37)/(2\pi * 0.127)`

`d=1.68* 10^(-3)\ m`

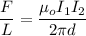
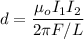
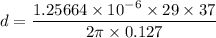
So, the distance of separation between the wires is
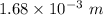`1.68* 10^(-3)\ m`. Hence, this is the required solution.