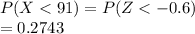Answer:
0.0010,0.2743
Explanation:
Given that Stanford–Binet IQ Test scores are normally distributed with a mean score of 100 and a standard deviation of 15
If x represents the scores then
X is N(100,15)
a) See enclosed file
b) Z score =
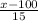
c) the probability that a randomly selected person has an IQ test score
i. Over 145.
=
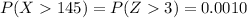
ii. Under 91
=