Question

Two identical circular, wire loops 48.0 cm in diameter each carry a current of 4.50 A in the same direction. These loops are parallel to each other and are 30.0 cm apart. Line ab is normal to the plane of the loops and passes through their centers. A proton is fired at 2600 m/s perpendicular to line ab from a point midway between the centers of the loops. Part A Find the magnitude of the magnetic force these loops exert on the proton just after it is fired. FF = nothing N

Answer 1

Step-by-step explanation:

It is given that,

Diameter of loops, d = 48 cm = 0.48 m

Radius of the loop, r = 0.24 m

Current carried in the loop, I = 4.5 A

Distance between loops, x = 30 cm = 0.3 m

Speed of the proton, v = 2600 m/s

We know that the magnetic field at the midway of the coils is given by :

`B=(\mu_o Ir^2)/((r^2+x^2)^(3/2))`

`B=(4\pi * 10^(-7)* 4.5* (0.24)^2)/(((0.24)^2+(0.3/2)^2)^(3/2))`

`B=1.43* 10^(-5)\ T`

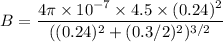
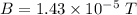
Let F is the magnetic force these loops exert on the proton just after it is fired. It is given by :

`F=q* v* B`

`F=1.6* 10^(-19)* 2600* 1.43* 10^(-5)`

`F=5.94* 10^(-21)\ N`

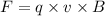
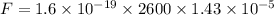
So, the magnetic force these loops exert on the proton is
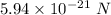`5.94* 10^(-21)\ N`. Hence, this is the required solution.