Question

A 500 kg block is attached to a horizontal spring that is at its equilibrium length, and whose force constant is 30 N/m. The block rests on a frictionless surface. A 600 kg wad of putty is thrown horizontally at the block, hitting it with a speed of 4.4 m/s and sticking. How far does the putty-block system compress the spring?

Answer 1

x = 0.396 m

Step-by-step explanation:

The best way to solve this problem is to divide it into two parts: one for the clash of the putty with the block and another when the system (putty + block) compresses it is spring

Data the putty has a mass m1 and velocity vo1, the block has a mass m2 . t's start using the moment to find the system speed.

Let's form a system consisting of putty and block; For this system the forces during the crash are internal and the moment is preserved. Let's write the moment before the crash

p₀ = m1 v₀₁

Moment after shock

`p_(f)` = (m1 + m2)
`v_(f)`

p₀ =
`p_(f)`

m1 v₀₁ = (m1 + m2)
`v_(f)`

`v_(f)` = v₀₁ m1 / (m1 + m2)

`v_(f)`= 4.4 600 / (600 + 500)

`v_(f)` = 2.4 m / s

With this speed the putty + block system compresses the spring, let's use energy conservation for this second part, write the mechanical energy before and after compressing the spring

Before compressing the spring

Em₀ = K = ½ (m1 + m2)
`v_(f)`²

After compressing the spring

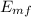`E_(mf)` = Ke = ½ k x²

As there is no rubbing the energy is conserved

Em₀ =
`E_(mf)`

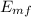
½ (m1 + m2)
`v_(f)`² = = ½ k x²

x =
`v_(f)` √ (k / (m1 + m2))

x = 2.4 √ (11/3000)

x = 0.396 m