Question

A farmer in Iowa owns 450 acres of land. He is going to plant each acre with wheat or corn. Each acre planted with wheat yields $2000 profit, requires three workers, and requires two tons of fertilizer. Each acre planted with corn yields $3000 profit, requires two workers, and requires four tons of fertilizer. There are currently 1000 workers and 1200 tons of fertilizer availab

Answer 1

each 200 acres.

Explanation:

Here we are given 2000 profit for wheat per acre and 3000 profit per acre for corn.

Hence objective function to maximize is

`Z=3000W+2000C`

Where W is wheat cultivated and C, corn cultivated

Constraints are workers and acres

Total workers required = 3W+2C and total fertilizers = 2w+4c

`3W+2C\leq 1000\\2W+4C\leq 1200`

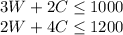
We solve and get corner points as

(W,C) = (333,0) (600,0) (0,500) (0,300)

Intersecting point is

by solving we get

2w = 400 or w =200 and c = 200

Thus feasible points are

(200,200) Or (333,0) or (0,300)

Z for I point = 1000000

Z for II point = 666000

Z for III point =900000

Maximum is when wheat and corn are 200 acres each planted.