Question

A group of students are provided with three objects all of the same mass and radius. The objects include a solid cylinder, a thin hoop (or cylindrical shell), and a solid sphere. The students are asked to predict which will get to the bottom of a ramp first if all three are released together from the same distance up the ramp. Which prediction is correct if the objects are listed in order from fastest to slowest?

Sphere (fastest), cylinder, hoop (slowest).

Sphere (fastest), hoop, cylinder (slowest).

Hoop (fastest), sphere, cylinder (slowest).

Hoop (fastest), cylinder, sphere (slowest).

Cylinder (fastest), hoop, sphere (slowest).

Cylinder (fastest), sphere, hoop (slowest).

No relationship can be predicted with the provided information.

Answer 1

Sphere, cylinder hoop

Step-by-step explanation:

To analyze Which student is right it is best to propose the solution of the problem. Let's look for the speed of the center of mass. Let's use the concept of mechanical energy

In the highest part of the ramp

Em₀ = U = mg y

In the lowest part

Here the energy has part of translation and part of rotation

`E_(mf)` =
`K_(T)` +
`K_(R)`

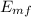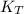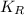
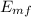`E_(mf)` = ½ m
`v_(cm)`² + ½ I w²

Where I is the moment of inertia of the body and w the angular velocity that relates to the velocity of the center of mass

`v_(cm)` = w r

w =
`v_(cm)` / r

Let's replace

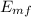`E_(mf)` = ½ I (
`v_(cm)` / r)²

Energy is conserved

mg y = ½ m
`v_(cm)`² + ½ I
`v_(cm)`² / r2

½ (m + I / r²)
`v_(cm)`² = m g y

½ (1 + I / m r²)
`v_(cm)`² = g y

`v_(cm)` = √ [2gy / (1 + I / mr²)]

This is the velocity of the center of mass of the bodies, as they all have the same radius with comparing this point is sufficient. Now let's use the speed definition

v = d / t

t = d / v

t = d / (√ [2gy / (1 + I / mr²)])

t = (d / √ 2gy) √(1 + I / m r²)

Therefore we see that time is proportional to the square root. All quantities are constant and the one that varies is the moment of inertia.

The moments of inertia of

Sphere is Is = 2/5 M r²

Cylinder Ic = ½ M r²

Hoop Ih = M r²

Let's replace each one and calculate the time

Sphere

ts = (d / √2gy) √ (1 + 2/5 Mr² / mr²)

ts = (d / √ 2gy) √ (1 +2/5) = (d / √ 2gy) √(1.4)

ts = (d / √ 2gy) 1.1

Cylinder

tc = (d / √2gy) √ (1 + 1/2 Mr² / Mr²)

tc = (d / √2gy) √ (1 + ½) = (d / √ 2gy) √ 1.5

tc = (d / √ 2gy) 1.2

Hoop

th = (d / √2gy) √ (1 + mr² / mr²)

th = (d / √2gy) √(1 + 1) = (d / √ 2gy) √ 2

th = (d / √ 2gy) 1.41

We have the results for the time the body that arrives the fastest is the sphere and the one that is the most hoop. Therefore the correct answer is

ts < tc < th

Sphere, cylinder hoop