Question

A manufacturer considers his production process to be out of control when defects exceed 4) 3%. In a random sample of 85 items, the defect rate is 5.9% but the manager claims that this is only a sample fluctuation and production is not really out of control. At the 0.01 level of significance, test the manager's claim.

Answer 1

To test the manager's claim about the defect rate not exceeding 3%, a hypothesis test can be performed using the observed defect rate of 5.9% in a sample of 85 items. The null hypothesis suggests a defect rate of 3% or less, and the alternative that it's higher. The test statistic is calculated to make the comparison.

Step-by-step explanation:

To test the manager's claim that the production process is not out of control at the 0.01 level of significance, we would perform a hypothesis test. The null hypothesis (H0) is that the defect rate is 3% or less, and the alternative hypothesis (H1) is that the defect rate is greater than 3%. Given a sample size (n) of 85 items and an observed defect rate of 5.9%, we can calculate the test statistic to compare against the critical value for this level of significance.

First, we calculate the expected number of defects:

• Expected defects = n * 0.03 = 85 * 0.03 = 2.55 defects

Next, we find the observed number of defects:

• Observed defects = n * 0.059 = 85 * 0.059 = 5 defects

The test statistic is normally distributed because we are dealing with proportions. We can calculate it as:

Z = (p‑hat - p0) / sqrt(p0(1‑p0)/n)

Where p‑hat is the sample proportion of defects 5.9% (0.059) and p0 is the assumed population proportion of 3% (0.03).

Answer 2

If, p-value<α reject the null hypothesis, hence the production process is not really out of control.

Step-by-step explanation:

From the information, observe that a manufacturer considers his production process to be out of control when defects exceeds 3%. Consider a random sample of 85 items, the defect rate is 5.9%.

Here, The claim is that this is the only sample fluctuation and production is not really out of control.

Consider a null and alternative hypothesis:

Null hypothesis, H_o: The production process is not out of control when the defect does not exceed 3%.

that is H_o: p<=0.03

Alternative hypothesis, H_a: the production process to be out of control when defect exceeds 3%

That is H_a: p>0.03:

Level of significance α= 0.01

Test statistics under null hypothesis.
`z= \frac{p-p}{\sqrt{(pq)/(n) } }`

`z= \frac{0.059-0.03}{\sqrt{(0.03(1-0.03))/(85) } }`

=
`(0.029)/(0.0185)`

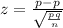
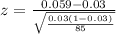
= 1.57

Calculative p-values as follows

P(z>1.57)= 1-P(z<=1.57)

= 1-0.9418

=0.0582

compare the p value with level significance

If, p-value<α reject the null hypothesis, hence the production process is not really out of control.