Question

Over the past several years, the owner of a boutique on Aspen Avenue has observed a pattern in the amount of revenue for the store. The revenue reaches a maximum of about $ 59000 in April and a minimum of about $ 29000 in October. Suppose the months are numbered 1 through 12, and write a function of the form f(x)=Asin(B[x−C])+D that models the boutique's revenue during the year, where x corresponds to the month.

Answer 1

`f(x) = -15000\sin [(\pi)/(6)(x-7)] + 44000`

Explanation:

Given, the function that shows the revenue.

`f(x) = A\sin [B(x-C)] + D`,

Where, x corresponds to the month.

∵ Revenue reaches a maximum of about $ 59000 in April and a minimum of about $ 29000 in October,

i.e. the maximum value f(x) is $ 59000 when x = 4,

And, the minimum value f(x) is $ 29000 when x = 10,

So, the amplitude,

`A = (max - min)/(2) = (59000 - 29000)/(2) = (30000)/(2)=15000`

`D = (max + min)/(2)=(59000 + 29000)/(2) = (88000)/(2)=44000`

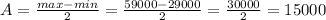
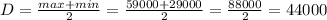
The minimum of sine function corresponds to
`-(\pi)/(2)`, here it is 10 and maximum
`(\pi)/(2)`, here it is 4.

Period = 12 months,

But we know period =
`(2\pi)/(B)`

`\implies (2\pi)/(B) = 12`

`\implies B = (\pi)/(6)`

∵
`(4+10)/(2) = (14)/(2)= 7`,

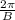
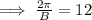
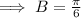
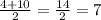Thus, f(x) is symmetrical about x=7,

⇒ C = 7,

Also, f(x) is minimum at x = 10,

So, A = - 15000,

Hence, the required function would be,

`f(x) = -15000\sin [(\pi)/(6)(x-7)] + 44000`