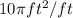Answer:
Option c)
10π ft^2/ft
Explanation:
Area of the circular puddle = A
=
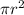
Where r is the radius of the circular puddle
Since the area of the circular puddle is constantly changing with respect to radius
Therefore, the differential equation hence formed will be
=
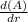
On putting the value of A
=
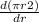
On differentiating
= 2πr
Hence , Area= A= 2πr
Putting the value of r = 5ft
Area =
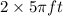
=