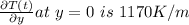Question

A 5-mm-thick stainless steel strip (k = 21 W/m•K, rho = 8000 kg/m3, and cp = 570 J/kg•K) is being heat treated as it moves through a furnace at a speed of 1 cm/s. The air temperature in the furnace is maintained at 1020°C with a convection heat transfer coefficient of 80 W/m2•K. If the furnace length is 3 m and the stainless steel strip enters it at 20°C, determine the temperature of the strip as it exits the furnace.

Answer 1

`(\partial T(t))/(\partial y) at\ y = 0\ is \ 1170 K/m`

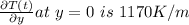
Step-by-step explanation:

we know that biot number is given as

`Bi = (hLc)/(k)`

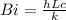
where Lc is characteristics length

`Lc = (v)/(A) = (LA)/(2A) =\frac[5}{2} = 2.5 mm`

`bI = (80* 2.5* 10^(-3))/(21) = 0.00952`

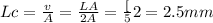
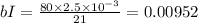
as biot number is less than 0.1 thus apply lumper analysis to find time constant t

`b =(hA)/(\rho V Cp) = (h)/(\rho Lc Cp)`

`b = ( 80)/(8000* 2.5* 10^(-3) \time 570) = 0.007018 s^(-1)`

`t = ((3)/(2))/(0.01) = 150 s`

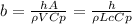
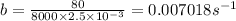
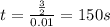
considerig temperature distiribution

temperature at mid length of furnase is

`(T(t) -T_(\infity))/(20 - T_(\infity)) =E^(-bt)`

`(T(t) -900)/(20 - 900) =E^(-0.007018* 150)`

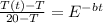
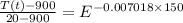
T(t) = 592.885 degree c

from Newton's law of cooling determine temp gradient at surface at t = 150 s

`-k (\partial T(t))/(\partial y) \at\ y = 0 is  h[T(t) -T_(\infity)]`

`(\partial T(t))/(\partial y) \ at\ y = 0 is (h[T(t) -T_(\infity)])/(k)`

`(\partial T(t))/(\partial y)\ at\ y = 0 is ( 80[592.885 - 900])/(21)`

`(\partial T(t))/(\partial y) at\ y = 0\ is \ 1170 K/m`